3D Registration is a fundamental part of several robotics and automation tasks. While classical methods predominantly exploit constraints from points or plane correspondences, we have a different take using line intersections. In other words, we focus on exploiting geometric constraints arising from the intersection of two (different) 3D line segments in two scans. In particular, we derive nine minimal solvers from various geometric constraints arising from line intersections along with other constraints: plane correspondences, point correspondences, and line matches. We follow a two-step method for 3D registration: a coarse estimation with outlier rejection followed by refinement. In the first step, we use a hybrid RANSAC loop that utilizes all the minimal solvers. This RANSAC outputs a rough estimate for the 3D registration and the outlier/inlier classification for the 3D features. As for the refinement, we offer a non-linear technique using all the inliers obtained from the RANSAC and the coarse estimate. This method is of alternate minimization type, in which we alternate between estimating the rotation and the translation at each step. Thorough experiments with simulated data and two real-world datasets show that using these features and the combined solvers improves accuracy and is faster than the baselines.

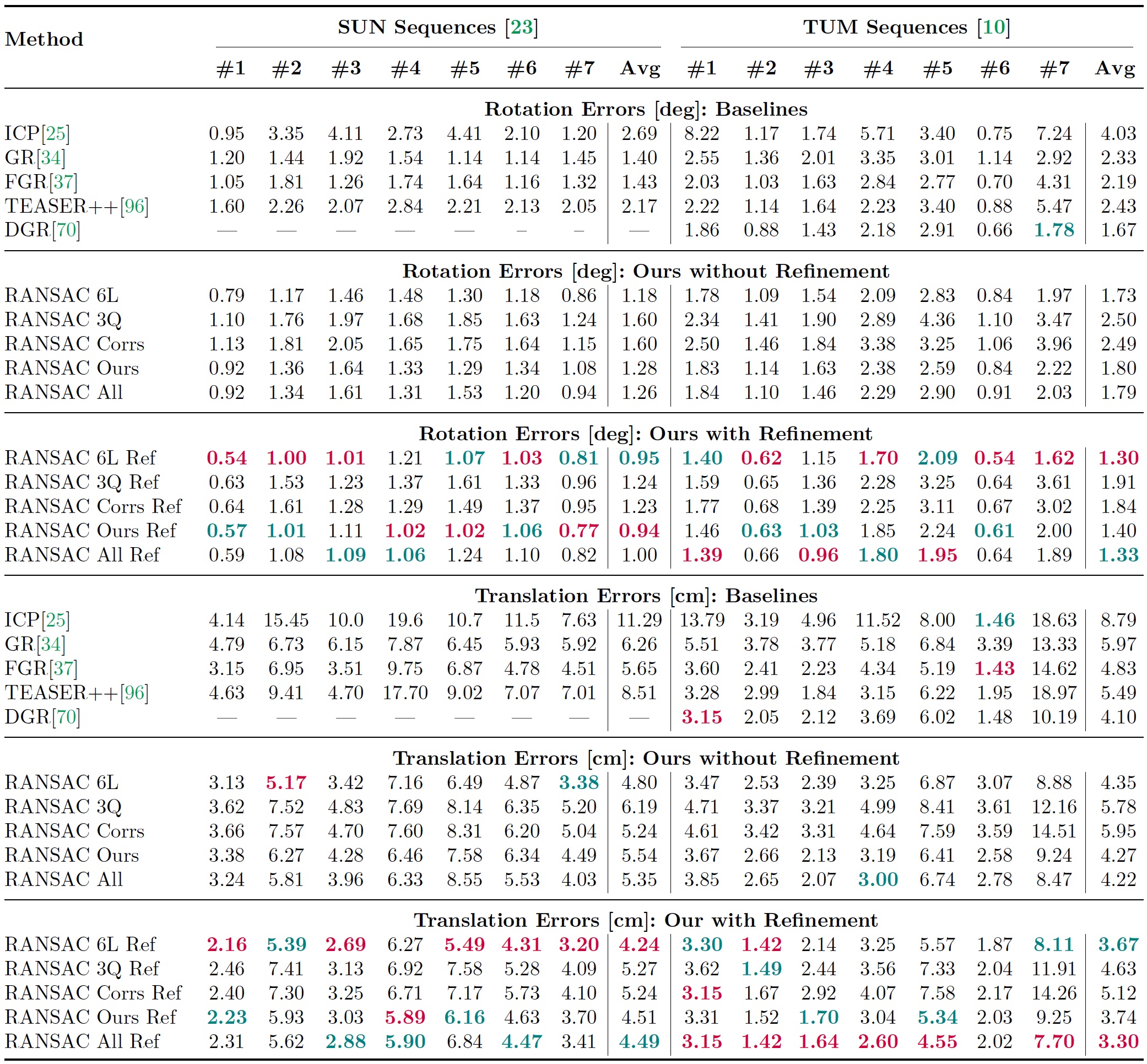
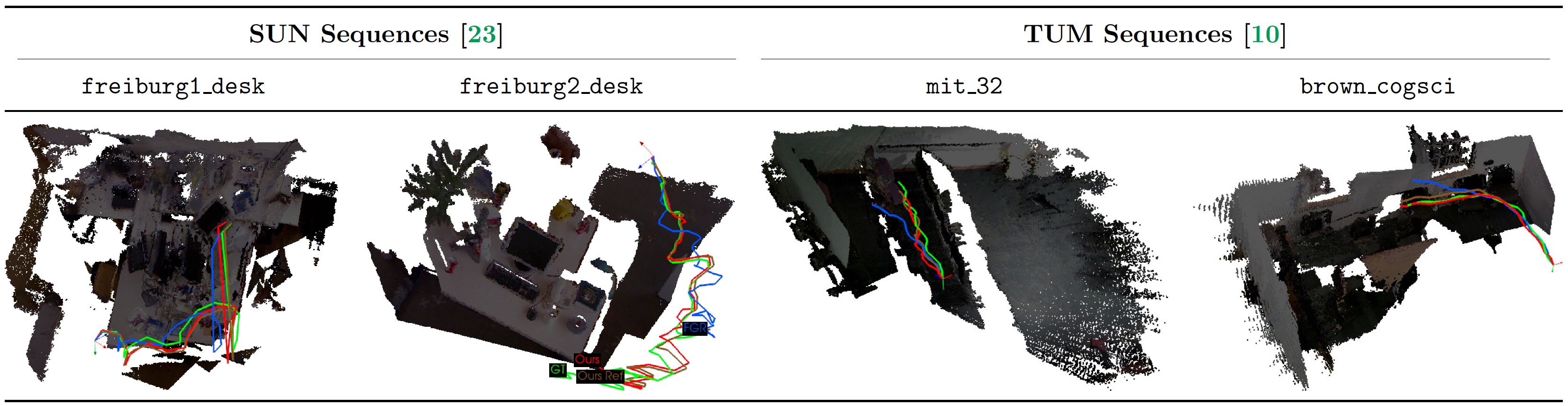
Our two-step method is a coarse and fine estimation approach. While the coarse estimate already provides good results, we see that our alternative minimization refinement approach, in general, is able to improve the accuracy significantly. For example, RANSAC Ours Ref is outperformed by the baselines in only two of the 14 sequences. More critical than that, when our two-step approach using line intersections is better than the baselines, the refinement can improve the results significantly with respect to the coarse approach obtained from RANSAC. For example, when compared to the baselines, we have improvements of around 48% in rotation and 31% in translation for the TUM sequence #7; 42% in rotation and 24% in translation in SUN sequence #1. We see that the proposed refinement technique has a minor impact on the computation time. The conclusions outlined for our strategy without refinement are kept for our approach with refinement. For example, RANSAC Ours Ref is only slightly slower than FGR, and about three times faster than DGR.
@article{Mateus23,
author = {Andr{\'e} Mateus and Siddhant Ranade and
Srikumar Ramalingam and Pedro Miraldo},
journal = {International Journal of Computer Vision},
number = {8},
pages = {2044--2069},
title = {Fast and Accurate 3D Registration from Line Intersection Constraints},
volume = {131},
year = {2023},
doi = {10.1007/s11263-023-01774-1},
}
@InProceedings{Mateus20,
author = {Andr{\'e} Mateus and Srikumar Ramalingam and Pedro Miraldo},
booktitle = {IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
title = {Minimal Solvers for 3D Scan Alignment With Pairs of Intersecting Lines},
year = {2020},
volume = {},
issn = {},
pages = {7232-7242},
doi = {10.1109/CVPR42600.2020.00726},
}
@InProceedings{Ranade20,
author = {Siddhant Ranade and Xin Yu and Shantnu Kakkar and
Pedro Miraldo and Srikumar Ramalingam},
booktitle = {Asian Conference on Computer Vision (ACCV)},
pages = {295--313},
title = {Mapping of Sparse 3D Data Using Alternating Projection},
year = {2021},
doi = {10.1007/978-3-030-69525-5_18},
}